Buongiorno a tutti, in questo blog ci occuperemo di come rappresentare graficamente variabili quantitative con Tableau Desktop. Successivamente andremo a interpretare il risultato finale da un punto di vista prettamente tecnico-statistico.
Con variabili quantitative si intendono tutti quei campi misurabili numericamente; esse si dividono in variabili continue (caratterizzate da un supporto continuo, ne è un esempio il peso) e discrete (caratterizzate da un supporto discreto, ne è un esempio il numero di figli che una persona può avere).
Per convenzione al tipo di grafico che andremo a studiare, in questo blog ci occuperemo solo delle prime.
Scatter plot: Cos’è?
Lo scatter plot ci permette di visualizzare la nuvola di punti rappresentante la nostra popolazione oggetto di studio, fornendoci la misura della correlazione (i.e. dipendenza lineare) che intercorre tra le variabili in questione.
Inoltre ci dà un’idea sull’andamento generale delle osservazioni statistiche; potrebbero esserci due (o più) nuvole di punti ben definite. In tal caso la popolazione risulterebbe “gruppata” secondo una logica ben precisa (solitamente se nel dataset vi è una variabile dicotomica, come ad esempio il gender).
Infine lo scatter plot ci permette di individuare visivamente eventuali outlier, cioè valori anomali che si discostano dal baricentro della nostra distribuzione e che necessitano di trattamenti specifici.
Scatter plot: Costruzione in Tableau
Per costruire questo grafico abbiamo bisogno di due variabili quantitative continue (measures) e di almeno una qualitativa (dimension) all’interno del nostro database.
Per iniziare carichiamo il dataset su Tableau Desktop e apriamo una sheet vuota. Successivamente creiamo il piano cartesiamo trascinando una measure in columns e una in rows.
Ora abbiamo bisogno di una dimension in Detail nel riquadro Marks per permettere al software di identificare ciascun punto.
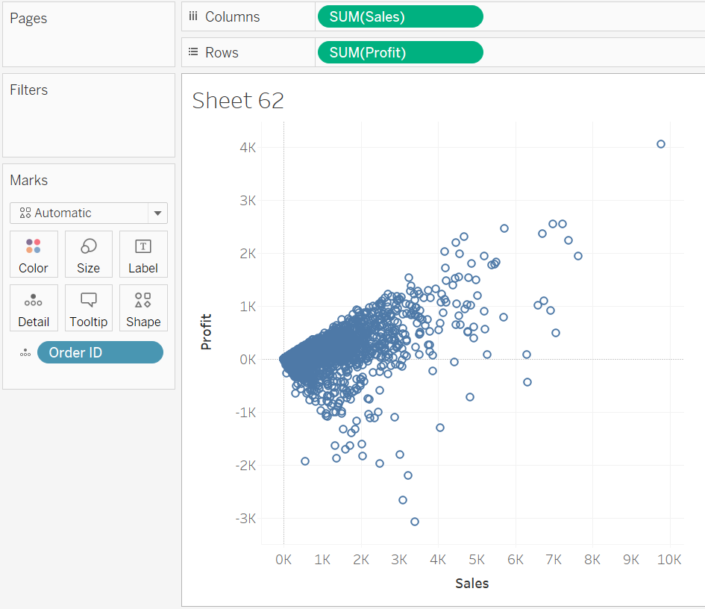
Attenzione: con l’asse delle ordinate dobbiamo rappresentare la variabile “risposta”, cioè quella dipendente dalla variabile rappresentata con l’asse delle ascisse, che sarà appunto la nostra variabile indipendente o “esplicativa”.
Il nostro obiettivo è spiegare l’andamento della variabile risposta grazie all’esplicativa. Nel nostro caso specifico vorremmo spiegare il profitto di un azienda in base alle vendite, ossia se all’aumentare delle vendite, aumenta anche il profitto.
Scambiare il ruolo delle due variabili produrrebbe lo stesso grafico ma specchiato rispetto alla bisettrice e non convenzionale per ciò che concerne l’interpretazione del comportamento dei due campi.
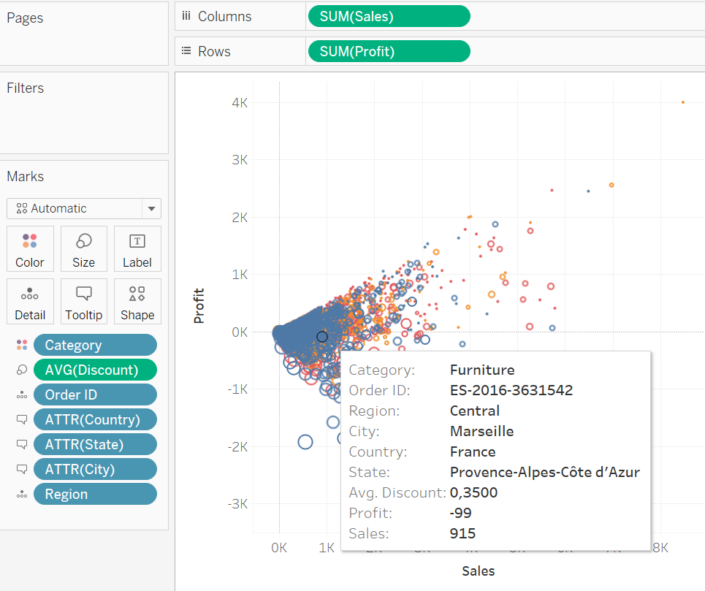
Tableau ci permette di arricchire il nostro scatter plot aggiungendo ulteriori particolari visivi.
Possiamo colorare i nostri punti in base a una variabile categorica trascinandola in Color, distinguerli con segni diversi trascinando un’altra variabile (o anche la stessa) in Shape e modificarne la dimensione trascinando una measure in Size.
È possibile anche aggiungere quante variabili si desidera in Tooltip. Se col cursore andiamo su un punto qualsiasi Tableau ci fornisce l’identità di quell’osservazione con le informazioni che abbiamo appena utilizzato.
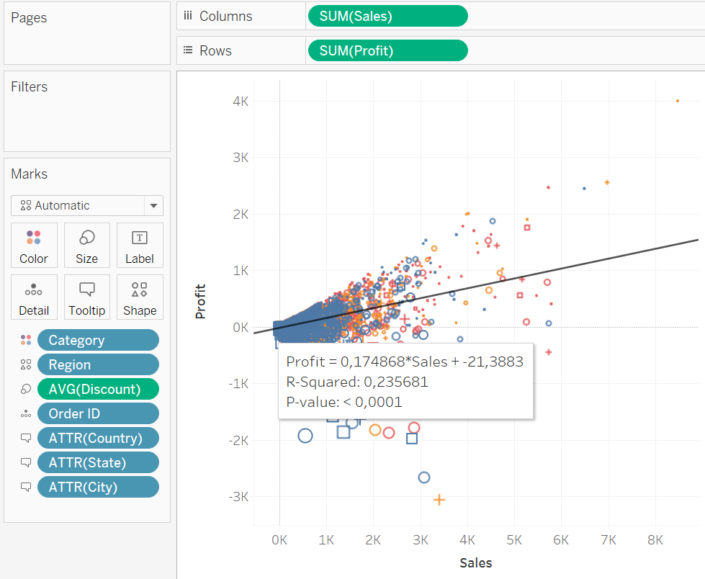
Ai fini dell’analisi statistica dobbiamo completare il grafico con una retta di regressione. Dal menù Analytics trasciniamo Trend line in Linear. Questa retta è quella che meglio approssima la nostra distribuzione.
Scatter plot: Analisi statistica
Se andiamo sulla retta di regressione col cursore Tableau ci fornisce svariate informazioni:
- L’equazione matematica della retta interpolante: Profit= 0,17*Sales+21,38. Più questa retta si avvicina a tutti i punti contemporaneamente più la sua capacità di approssimazione è soddisfacente.
- Il valore dell’R-quadro: 0,23. Esso è un indice di bontà del modello statistico che stiamo analizzando. E’ normalizzato, cioè compreso tra 0 e 1. Più si avvicina a 1 più il mio modello è un buon modello, più si avvicina a 0 più è un pessimo modello. Casi estremi: se R-quadro=0 la variabile esplicativa non spiega niente della variabile risposta, se R-quadro=1 tra le due variabili vi è una dipendenza perfetta (massima correlazione).
- Il valore del P-value: <0,0001. Esso è lo strumento di cui ci serviamo per accettare o rifiutare il modello statistico (cioè la retta di regressione come approssimazione dei nostri punti). Più il p-value è piccolo, più la variabile indipendente è utile a spiegare quella dipendente (più il mio modello è un buono).
In conclusione, nel caso in figura, osserviamo un R-quadro non eccessivamente alto. Di fatti i nostri punti non sembrano seguire un andamento sistematicamente lineare. Tuttavia il P-value risulta essere estremamente significativo, quindi accettiamo il modello. Le vendite ci sono utili per spiegare il profitto della nostra azienda in esame.



























