Data –Predicting Churn for Bank Customers
Naive Bayes è un modello probabilistico che assegna la probabilità di un evento calcolando la probabilità individuale delle variabili.
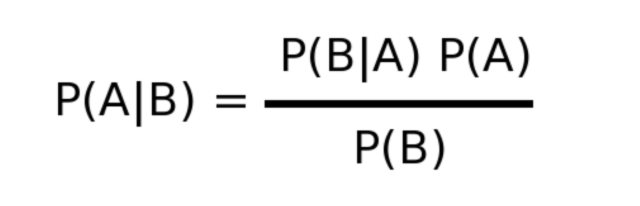
P(a|b) = A è la churning prediction del cliente se si verifica B, dove B sono le variabili del nostro dataset come Tenure, Age,Credit Score.
Per esempio: si verificherà churning con un cliente di 30 anni e un credit score di 350 e 2 anni di tenure.
P(a|b) viene calcolato su alcune probabilità individuali, per questo è chiamato Naive, perchè assume ogni variabile indipendentemente dalle altre.
P(b|a) è la probabilità dell’evento B se A si è già verificato (per esempio, se il cliente ha 18 anni e abbiamo un dataset di vecchi clienti che hanno abbandonato la banca, possiamo creare una probabilità che rispecchia la probabilità di customer churning se il cliente ha 18 anni). Questo vale per tutte le variabili come tenure, credit, score ecc.
P(A) = probabilità di customer churning: se sappiamo che 100 clienti su 1000 lasceranno la banca allora la probabilità è di 100/1000.
P(B) = probabilità delle variabili. Per esempio qual è la probabilità che un cliente avvia 18 anni rispetto a tutti gli altri clienti.
Dobbiamo calcolare la probabilità P(a/b) sia di abbandono (Churn) e sia di non abbandono (Retained) allo stesso modo e poi normalizzare entrambi i numeri. Quindi la probabilità con il numero maggiore sarà la risposta.
Se Normalized P(a|b)(churn) > Normalized P(a|b)(Retained) allora il cliente abbandonerà la banca.
Anche Possiamo modificare la formula per un’implementazione più semplice su Tableau.
- P(B) è il denominatore che è costante quindi non dobbiamo calcolarlo perchè non influirà nell’analisi.
- Moltiplicando multiple probabilità (ad esempio P(age|churn)*P(tenure|churn)*P(a) darà come risultato un numero molto piccolo e richiederà un’elevata capacità computazionale. Una soluzione può essere utilizzare un trucco matematico utilizzando la funzione logaritmo per sommare invece di moltiplicare:
Churn: LOG(P age|churn) +LOG((P tenure|churn)+LOG(P churn)
Retained:LOG(P age|retained) +LOG((P tenure|retained)+LOG(P retained)
Implementazione sul Tableau
- Data exploration e Feature engineering: il primo passaggio è esplorare i dati e trovare le informazioni rilevanti per il customer churning e usare quelle variabili in accordo con il “Bias Variance Trade off” per cui non vogliamo usare troppe variabili che aumenteranno la varianza e Overfitting il modello e non vogliamo neanche fare un modello troppo semplice basato su una variabile che coomporta un aumento di bias e Underfitting
In accordo con i miei risultati, ho utilizzato queste variabili:Income to Debt={FIXED [Credit Score],[Tenure] :sum ( [ Estimated Salary])}Credit Score by Age= [Credit Score]/[Age] - il nostro obiettivo è minimizzare i falsi positivi e aumentare i veri negativi oppure minimizzare i falsi negativi e aumentare i veri positivi, a seconda di quello che vogliamo ottenere con l’analisi.
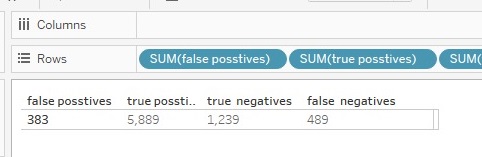
Il mio modello dà come risultato 5889 + 383persone che non lasceranno la banca, dove 5889 rappresenta le previsioni accurate e 383 quelle non corrette e uguale per persone che laciarano 1239+489
Calcoli per refrenze-Step by step
Churn- if [Exited]=1 then 1 ELSE 0 ENDRetained-if [Exited]=0 then 1 ELSE 0 ENDIncome to Debt={FIXED [Credit Score],[Tenure] :sum ( [ Estimated Salary])}Credit Score by Age= [Credit Score]/[Age]P Churn (P(A))={SUM([Churn])}/{COUNT([Customer Id])}P Retained (P(A))={SUM([Retained])}/{COUNT([Customer Id])}P(Income to Debt|Churn)={ FIXED [Income to debt]:SUM([Churn])}/{SUM([Churn])}P(Income to Debt|Retained)={ FIXED [Income to debt]:SUM([Retained])}/{SUM([Retained])}Ripetre Step 7 e 8 per tutti variabli selezionate ,in mio caso(Income to Debt e Credit score by age)Naive Bayes Churn=LOG(P(Income to Debt|Churn))+LOG(P(Credit score by age|Churn))Naive Bayes Retained=LOG(P(Income to Debt|Retained))+LOG(P(Credit score by age|Retained))Normalize Naive bayes Churn=[Naive Bayes Churn]/[Naive Bayes Churn ]+[Naive Bayes Retained]Normalize Naive bayes Retained=[Naive Bayes Retained]/[Naive Bayes Churn ]+[Naive Bayes Retained]Predizione=IF [Normalize Naive bayes Churn]>[Normalize Naive bayes Retained ] THEN 1 ELSE 0 END
Model Accuracy Check
Dopo aver eseguito le formule possiamo calcolare accuratezza del modello:
Retained Predizione=if [Predizione]=0 then 1 ELSE 0 END
Churn Predizione=if [Predizione]=1 then 1 ELSE 0 END
1-False Positive : clienti che il modello aveva previsto non avrebbero lasciato la banca ma che in realtà hanno lasciato.
if { FIXED [Customer Id]:sum([Retained])} < {FIXED [Customer Id]:SUM([Retained Predizione])} THEN 1 ELSE 0 END
2-False Negatives: clienti che il modello aveva previsto avrebbero lasciato la banca ma che in realtà non hanno lasciato.
if { INCLUDE [Customer Id],[Exited]:sum([Retained])}=1 AND zn({include [Customer Id],[Predizione]:SUM([Retained Predizione])})=0 THEN 1 ELSE 0 END
3-True Possitives : numero di persone che non hanno lasciato la banca che il modello ha identificato correttamente;
if { INCLUDE [Customer Id],[Exited]:sum([Retained])}=1 AND {include [Customer Id],[Predizione]:SUM([Retaine predictor ])}=1 THEN 1 ELSE 0 END
4-True Negatives = numero di persone che hanno lasciato la banca correttamente identificate dal modello.if { INCLUDE [Customer Id],[Exited]:sum([Churn])}=1 AND {include [Customer Id],[Predizione]:SUM([Churn predizione])}=1 THEN 1 ELSE 0 END
Dopo aver bilanciato i falsi positivi e i falsi negativi e aver ottenuto il miglior modello in accordo con i nostri requisiti e il nostro il business possiamo creare una dashboard che fa previsioni creando parametri, dove l’utente può inserire le variabili da usare (come età, tenure, credit score) e il modello calcolerà P(A/B) per i dati inseriti .
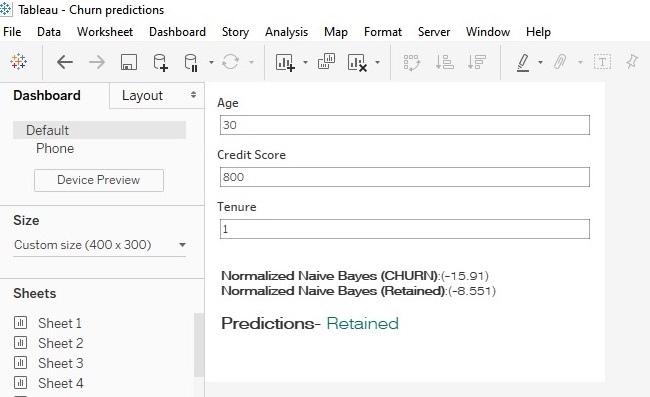
Calcoli Cambiano Per parametri–
Income to Debt={ FIXED [Parameters].[Credit Score]=[Credit Score],[Parameters].[Tenure]=[Tenure]:sum([Estimated Salary])}Credit Score by Age= { FIXED [Parameters].[Credit Score]=[Credit Score],[Parameters].[Age]=[Age]:sum([Credit Score])/sum([Age])}



























